
Patmos
Site de l'écrivain Marc D'Angelo
La quatrième chambre de Khéops
Une hypothèse sur l'emplacement d'une chambre inconnue dans la Grande pyramide, d'après des observations et des spéculations géométriques
Les technologies les plus novatrices ont été mises à contribution, dans le cadre de la mission Scan Pyramids, pour tenter d'apporter une réponse à la question qui agite depuis toujours l'égyptologie : existe-t-il, dans la Grande Pyramide, une chambre cachée (ou plusieurs) ? Ce projet se donne pour ambition de déterminer l'emplacement de cette ou de ces cavité(s) hypothétique(s), s'il y en a, en faisant intervenir en particulier la radiographie par muons.
Les chercheurs qui ont émis des hypothèses concernant la "chambre secrète de Khéops" espèrent les voir validées par cette mission. Philippe Lheureux, par exemple, en attend beaucoup : selon lui, elle confirmera la présence d'une chambre dont il annonce la présence, depuis plusieurs années, dans le voisinage immédiat de la Chambre dite "du Roi".
Je doute, pour ma part, que cette chambre tant attendue soit située dans la maçonnerie du monument, même si ce n'est pas une possibilité qu'il faut exclure a priori. Mes propres recherches m'incitent à penser, en effet, qu'elle devrait plutôt se trouver, si elle existe, dans la partie souterraine.
J'ai déjà formulé des propositions, à ce sujet, dans le magazine Nexus (n°95, nov.-déc. 2014). Je les réitère ici, en leur adjoignant quelques éléments complémentaires.

Plan en coupe de la Grande Pyramide, dessiné par Franck Monnier à partir des relevés et des mesures de Gilles Dormion. Il montre, d'après une coupe nord/sud, les structures actuellement connues : Chambre "du "Roi", "de la Reine", Chambre souterraine, Grande Galerie, Couloir ascendant, Couloir descendant, Couloir horizontal... Désignés par 10 et 7 : les conduits dits "d'aération", dont on pourra démontrer l'implication prépondérante dans la conception géométrique du monuments.
Dans le contexte géométrique de la Grande Pyramide, les conduits dits "d'aération" ou "de ventilation" jouent un rôle majeur. Ces minces canaux (20 cm x 20 cm), n'ayant de "ventilatoires" que la fonction qui leur a été assignée par défaut et contre toute vraisemblance, entrent de façon déterminante dans le plan d'ensemble.
Il est possible de donner, sur la base des éléments apparents, d'une part, et, d'autre part, au prix de quelques déductions et spéculations simples, une "justification" géométrique à la position des structures connues, à commencer par la Chambre dite "du Roi", dont l'emplacement est indubitablement déterminé en fonction du fameux Nombre d'Or. Ce sont les conduits "d'aération" qui vont, en grande partie, permettre cette "justification". De même, ce sont eux qui vont rendre possible des propositions concernant la position théorique de structures aujourd'hui non-identifiées. Autrement dit, par l'analyse et spéculation géométriques, en découvrant de multiples correspondances entre une structure donnée de la Grande Pyramide et une coordonnée géométrique, nous pouvons décrypter plus efficacement le mystérieux édifice dont certains aspects conceptuels se font jour ainsi, et, de plus, nous pouvons envisager des pistes pour la recherche de ses parties encore inconnues.
Sur la figure ci-dessous, on peut voir un exemple de justification géométrique de la position du Couloir descendant. La figure semble un peu complexe de prime abord, mais au final l'argument apparaîtra plutôt simple.
Considérons les données de cette figure dans l'ordre suivant : Nous voyons deux grands cercles ; ils ont l'un et l'autre pour centre respectifs chacun des angles de base de la pyramide, et pour rayon sa demi-base ; autrement, dit leurs rayons horizontaux qui se dirigent l'un vers l'autre, l'un vers le sud (vers la gauche du dessin) et l'autre vers la nord (la droite du dessin), se rejoignent au milieu de la base du monument.
En rouge, nous avons un "Carré long" (figure fondamentale de la géométrie sacrée ; voir le lien ci-dessous). Comment, à partir de quels paramètres, ce rectangle est-il construit ? Nous ne l'avons pas dessiné et placé "au hasard"... Il est déterminé et positionné d'après ce que nous pouvons appeler le triangle pyramidal, c'est-à-dire le triangle dont les proportions et les dimensions sont celles du triangle du monument lui-même. En l'occurrence, nous avons "utilisé" ce triangle pyramidal en le plaçant, à l'envers, au-dessous de la ligne de base, comme un reflet inversé du triangle de la pyramide elle-même. De cette manière, nous obtenons, avec la pointe du triangle (équivalent du sommet de la pyramide mais dans le sous-sol virtuel), un point situé à la même distance de la ligne de base que le sommet.
Ensuite, nous prolongeons les apothèmes de la pyramide, les lignes de ses faces telles que nous les voyons dans cette vue en coupe, jusqu'à ce qu'elles aboutissent au même niveau que le point donné par le "sommet inversé" ; nous pouvons donc tracer une ligne horizontale passant par ces trois points : le sommet inversé et la fin de chaque ligne, à droite et à gauche de notre figure.
Premier constat : les points où les lignes de prolongation des apothèmes intersectent la ligne horizontale définie par le sommet inversé, se trouvent à l'aplomb du bord "extérieur" (par rapport au monument) de chaque cercle. Ceci n'est possible qu'en fonction des dimensions et proportions du triangle pyramide tel que les bâtisseurs l'ont choisi.
Maintenant, "décidons" de faire de la ligne horizontale que nous avons obtenu par le sommet du triangle pyramidal inversé et la prolongation des apothèmes, le côté long, horizontal et inférieur d'un "carré long", c'est-dire d'un rectangle dans la surface est égale à celle de deux carrés placés côte-à-côte. Les côtés courts, verticaux seront donc tangents aux bords extérieurs des cercles. Et qu'allons-nous constater ? Que le côté long horizontal et supérieur de ce rectangle (de ce "carré long" comme on l'appelle en géométrie sacrée) passe par la ligne joignant les points de sortie des conduits d'aération de la Chambre "du Roi" ! Etonnant, non ?
Il apparaît que, dans ces conditions, l'une des diagonales, ci-dessous figurée en vert, reçoit exactement le Couloir Descendant.
Nous avons également noté, sur cette figure, quoique cela soit, a priori, de moindre importance, les diagonales d'un autre "Carré long", plus petit ; l'une d'entre elles, en vert aussi, est parallèle à la Grande Galerie et au Couloir ascendant. Ce parallélisme est naturel et obligé, pourrait-on dire, puisque ces deux structures ont une inclinaison pour ainsi dire égale à celle de la diagonale du "Carré long" (26°275). On peut observer néanmoins que cette ligne verte est située sur des zones où certains chercheurs voient une hypothétique voie d'accès "bis" à la Chambre dite "du Roi".

Il existe une relation du Carré long avec le Nombre d'Or, et elle concerne d'une façon assez étonnante les éléments du plan de la Pyramide évoqués ici. Voir le lien ci-dessous.
A partir de la position des éléments déjà répertoriés de l'architecture du monument - à commencer par la position des conduits eux-mêmes - on peut se risquer à localiser une "quatrième chambre", c'est-à-dire une salle virtuellement analogue aux trois que nous connaissons actuellement (pour mémoire, la Chambre dite "du Roi", la Chambre dite "de la Reine" et la Chambre souterraine).
Quoi que cette chambre hypothétique puisse contenir - et même si, comme ses trois homologues déjà connues, elle ne contient rien - les indices géométriques nous invitent à la situer dans la partie souterraine plutôt que dans la maçonnerie, où la plupart des chercheurs postulent sa présence. Ces indices nous sont fournis, en grande partie, par les pseudo-conduits "d'aération".
Les conduits sont au nombre de quatre, comme nous l'avons vu plus haut, et vont par paires : deux pour la Chambre "du Roi", deux pour la Chambre "de la Reine".
Ceux de la Chambre haute (dite "du Roi") traversent toute la maçonnerie et débouchent à l'extérieur, tandis que ceux de la Chambre médiane (dite "de la Reine") sont interrompus en-deçà de la paroi. (A leurs extrémités se trouvent les fameuses "portes" ou "dalles", dont la première a été découverte par le robot Upuaut de Rudolk Gantenbrink, en 1994.) Il y a, sans nul doute, une raison à cette "interruption" ; on la suppose d'ordre technique ou pratique. Mais, sur ce point comme sur tous les autres ou presque, on en est réduit aux hypothèses. Du point de vue géométrique, cependant, il est loisible d'établir certains constats.

Ci-dessus : cerclées en vert, les extrémités supérieures des conduits-Roi, débouchant à l'extérieur du monument ; cerclées en bleu, les extrémités supérieures des conduits-Reine, situées en-deçà des apothèmes.
On peut noter que l'inclinaison des conduits-Reine, respectivement de 37°28 pour le conduit nord et de 38°28 pour le conduit sud, correspond à 11/14, soit l'inverse du rapport de pente des apothèmes, qui est de 14/11. Par ailleurs, le conduit-Roi nord, pour une inclinaison de 32°30, correspond à un rapport de pente de 7/11.
Pour en savoir plus sur ces trois nombres associés : 7, 11 & 14, voir la Page intitulée Correspondances .
On peut tirer peut-être quelque chose d'intéressant et d'utile de cette disposition des quatre conduits (deux d'entre eux débouchant à l'extérieur, les deux autres interrompus avant) du point de vue conceptuel et symbolique, nonobstant l'ignorance dans laquelle nous nous trouvons de ses impératifs ou de ses fonctions techniques ou pratiques.
En effet, si les conduits-Reine ne vont pas physiquement jusqu'à l'extérieur, il ne fait guère de doute qu'ils atteignent virtuellement la surface du monument... Or, en les prolongeant de la sorte et en prenant en compte leurs points de sortie virtuels, il est possible de déterminer un carré, auquel on donne pour côté la ligne entre les points de sortie virtuels des conduits ; on peut procéder de même pour les conduits-Roi, à partir de leurs points de sortie réels. Nous appelons ces deux carrés : Carré-Roi et Carré-Reine.
(Notre attention a été attirée déjà, rappelons-le, sur le niveau des points de sortie des conduits-Roi, correspondant au bord supérieur du Carré long dont l'une des diagonales reçoit le Couloir descendant.)
Ci-dessous, le Carré-Roi en rouge et le Carré-Reine en bleu :

Le carré-Roi apparaît, pour la première fois (mais pas sous ce nom-là), dans Le Mystère du Grand Sphinx de Robert Bauval et Graham Hancock (cliquer ci-dessus pour plus d'infos).
Les diagonales du Carré-Roi se coupent au sommet de la voûte-Reine. Par ailleurs, étant donné que l'une de ces diagonales "emprunte" le conduit-Roi sud, celui-ci se trouve donc, en quelque sorte, "dirigé" vers ce point crucial du monument... (En outre, on peut noter que le sommet du plafond de la Chambre médiane se trouve un peu en-dessous du point commun des médiatrices du triangle.)
On voit également que les diagonales du Carré-Reine se croisent au niveau supposé du "sol". Il faut préciser que cette "ligne de sol" n'est que théorique ; certains pensent qu'elle est, en réalité, plus haute, dans la partie centrale, qu'il y a là une "butte" et que la Chambre médiane est "posée" dessus. Mais si, par chance pour Gilles Dormion et Franck Monnier qui l'ont ainsi imaginée et représentée, la "ligne de sol" réelle est, à peu de choses près, identique à celle-ci, il y aurait une coïncidence entre le centre du Carré-Reine et le point d'intersection du "sol" avec l'axe central.
Notons encore une propriété de cette disposition géométrique qui attire l'attention sur les conduits, et sur leurs points de sortie.
Comme on le voit sur la figure ci-dessous, les points de sortie des conduits-Roi se trouvent au point d'aboutissement des bissectrices sur les apothèmes. On aurait peine à considérer ceci comme fortuit et indifférent... Cette propriété essentielle et frappante n'a jamais été observée auparavant.

La figure suivante montre que le cercle circonscrit dans le triangle pyramidal, dont le centre se trouve au point commun des bissectrices, passe par les extrémités des conduits-Reine, qu'il semble ainsi "délimiter"...
Ainsi les bissectrices permettent-elles de déterminer à la fois l'extrémité des conduits-Roi et celle des conduits-Reine.
Pourquoi en est-il ainsi ? Nous l'ignorons, mais il paraît difficile, une nouvelle fois, de croire que cela serait dû au "hasard"...
On s'est beaucoup interrogé sur la disparité entre les conduits-Roi et les conduits-Roi, donc sur l'énigmatique raison qui a poussé les constructeurs à interrompre les seconds avant la surface, au contraire des premiers. Cette double propriété, liée aux bissectrices du triangle pyramidal, ne nous éclaire pas sur les mobiles de l'architecte à cet égard, mais elle nous renseigne sur certaines coordonnées géométriques auxquels répond leur disposition.

Une chose semble donc certaine : les conduits ont été construits d'après des paramètres et des préoccupations géométriques, avec, très probablement, le souci d'une cohérence et une attention portée à des concordances. Dans quel but exactement, dans quel contexte technique et en vertu de quelle "philosophie architecturale" ? Nous ne sommes pas en mesure de le dire, mais l'un des "visages" de la Pyramide, par là, se dévoile à nous...
Allons plus loin...
Il est tentant d'envisager que la dissymétrie entre les deux paires de conduits, dans leur partie finale, constitue comme une "invitation à la prolongation" : autrement dit, on pourrait songer qu'il faut pratiquer, avec d'autres éléments structurels, cet exercice de la "prolongation virtuelle", comme on l'a fait pour les conduits-Reine en les "faisant parvenir" jusqu'à la surface.
De fait, on discerne, en procédant ainsi, un ensemble de paramètres géométriques où se tisse un réseau de correspondances, et l'on voit apparaître la désignation d'un ou de plusieurs point(s) potentiellement porteurs d'autres structures. Cette "méthode" de la "prolongation virtuelle" est une clé pour l'analyse et l'exploration géométrique de Khéops, ouvrant de multiples pistes. Nous allons l'appliquer ici, tout d'abord aux conduits eux-mêmes.
L'exercice est assez simple : chaque conduit, comme n'importe quel segment de droite, ne peut être prolongé que dans deux directions.
Les conduits nord (-Roi et -Reine) et les conduits sud (-Roi et -Reine) n'ayant pas le même angle de pente, leurs droites prolongées convergent vers un point ; en ce point elles se rejoignent, et en ce point elles se coupent si on continue de les prolonger. Les résultats de nos observations tendent à démontrer, sans le moindre doute, qu'il faut "s'arrêter" au point de rencontre ; en d'autres termes, il faut prolonger jusqu'à la convergence, et ensuite il ne faut plus prolonger... Peut-être y a-t-il là quelque chose qui s'apparente à un "enseignement spirituel", traduit dans l'espace euclidien ; s'il n'est pas signifié à dessein, il est implicite, et l'on se plaît à y songer.
Mais revenons à la géométrie elle-même, et à l'identification, dans le monument qui nous occupe, de ses implications structurelles...
Les conduits sud convergent vers un point situé quelque peu au-dessous du niveau du sol sur lequel repose la base de la pyramide.
La détermination exacte de ce point est assez délicate, dans la mesure où l'évaluation de l'angle de pente exact du conduit-Reine peut être sujet à caution. (Pour celui du conduit nord, l'angle de 45° paraît s'imposer.)
Michel Sélaudoux, un auteur qui s'est passionné pour les aspects numériques et géométriques des monuments égyptiens, situe ce point comme on le voit sur le schéma ci-dessous :

Cette position semble intéressante, du fait que le point de convergence se trouve directement à l'aplomb de l'entrée de la Grande Galerie. Toutefois, c'est la seule correspondance susceptible de lui offrir une "légitimité" et un "intérêt". Elle est, me semble-t-il, insuffisante, d'autant qu'une autre position lui confèrera des propriétés plus convaincantes. Il ne s'agit pas toutefois, bien sûr, de le positionner pour qu'il satisfasse à certains critères, mais avec précision.
D'après les coordonnées fournies par Gilles Dormion (Gilles Dormion, La chambre de Chéops, 2004), nous le localisons comme suit :

On voit que le point de convergence, cerclé ci-dessus en vert, ne se situe pas à l'aplomb de l'entrée de la Grande Galerie. En revanche, il possède, dans cette position, d'autres propriétés fort intéressantes. Nous y reviendrons plus loin.
Les conduits nord, quant à eux, se rejoignent en un point situé bien au-dessus du sol et du monument lui-même, "dans le ciel", pourrait-on dire ; nous l'avons nommé "Point Focal Céleste".

Soit dit en passant, je ne vois vraiment pas comment John Legon, dont les travaux sont, à mon sens, surévalués, réussit à fixer le point de convergence des conduits nord à hauteur du sommet de la Pyramide... Son schéma figure sur une Page Wikipédia consacrée à l'Observation mathématique de la Grande Pyramide, dans une partie intitulée pompeusement Géométrie des conduits de ventilation. Une étude sérieuse et poussée montre qu'il y a bien, en effet, une "géométrie des conduits de ventilation", mais qu'elle ne se limite pas à de trop pauvres observations, erronées de surcroît. Les quelques considérations publiées ici suffisent à montrer - et elles sont loin d'être exhaustives - que l'étude des conduits constitue un domaine vaste et fécond.
Après avoir situé le Point Focal Céleste, faisons intervenir un paramètre supplémentaire : ne sommes-nous pas portés à considérer que le Puits, ou plus précisément sa portion rectiligne, la plus longue, représente l'équivalent d'un "troisième conduit" ? (Je suis redevable à Jean-Jacques Dugt de cette idée d'assimiler la portion rectiligne du Puits à un troisième conduit.)
Ci-dessous, la figuration de cette virtuelle équivalence :

Comme les conduits (dirigés vers la Chambre haute et la Chambre médiane, ou plus exactement vers leur "sous-sol"), cette section du Puits est "dirigée" vers une chambre (la Chambre souterraine, ou plus exactement, là encore, vers son "sous-sol"). Si on la prolonge virtuellement, elle aboutit au-dessous de la dite-chambre, de même queles conduits-Roi et -Reine (quoiqu'à un niveau sensiblement inférieur) aboutissent au-dessus des Chambres dites "du Roi" et "de la Reine".
Nous allons voir qu'elle est "dirigée", à son autre extrémité, cette ligne correspondant à la section rectiligne du Puits, vers le même point "céleste" que les deux conduits nord, moyennant une légère correction de son inclinaison...
Mais avant cela, voici ce qu'il en est si l'on n'opère pas la dite-correction. La ligne est tracée, ci-dessous, en pointillés bleus, selon l'inclinaison effective de la structure, soit 47°. On voit qu'ainsi cette ligne (que nous désignerons comme la "troisième droite") ne rejoint pas le point de convergence des deux conduits nord (cerclé en vert).

Pour qu'elle rejoigne les deux autres au même point focal, il faut donner à cette troisième ligne une valeur légèrement corrigée par rapport à la position exacte de la structure qu'elle supporte : c'est, en effet, avec une inclinaison de 45° (et non de 47°) qu'elle rejoint celle du conduit-Roi et celle du conduit-Reine.
On retrouve cet angle de 45°, qui n'est évidemment pas "n'importe quel angle" (c'est la moitié de l' "angle droit" de 90°), dans l'inclinaison du conduit-Roi sud, comme nous l'avons déjà vu plus haut, mais aussi par ailleurs, d'une autre manière, comme cela sera montré plus loin.
En optant pour cette inclinaison qui s'écarte de 2° de l'inclinaison mesurée du Puits dans sa portion rectiligne, on constate une convergence des trois droites qui, manifestement, ne peut être fortuite :

En réalité, donc, il ne s'agirait pas à proprement parler d'une "correction" : notre "troisième droite" n'apparaît pas "aux forceps", par suite d'une manipulation de données et au prix d'un décalage arbitraire de 2° ; elle existe, bel et bien, conceptuellement et préalablement, dans ce faisceau trinitaire, avec une inclinaison de 45°, et la structure avec laquelle elle est en rapport accuse par rapport à elle un décalage de 2°.
Une fois de plus, il doit y avoir une raison à cela... Et peut-être cette raison réside-t-elle, en partie, dans ce que nous voyons dans la figure ci-dessous :

A partir du point d'aboutissement, au-dessous de la Chambre souterraine, de la droite passant par la portion rectiligne du Puits, en valeur non corrigée de 47°, on peut tracer une ligne parallèle au Couloir descendant, passant par le point de convergence des conduits sud.
L'avenir des recherches nous dira peut-être si cela - comme le reste - est en rapport avec une structure aujourd'hui non identifiée.
(Il conviendrait aussi, sans doute, de déterminer une éventuelle correspondance du Point Focal Céleste avec une étoile, d'une part, et, d'autre part, avec un point situé sur le Plateau de Gizeh, en vertu de la correspondance d'ensemble mise au jour par Guy Gruais et Guy-Claude Mouny.)
L'assimilation du Puits, par analogie, à un "troisième conduit", et la détermination d'une troisième droite, analogue à celles des conduits, et dirigées, avec elles, vers un même point de convergence (le Point Focal Céleste), nous amènent tout naturellement, en quelque sorte, à concevoir la possibilité d'une quatrième droite, analogues aux trois précédentes ; cette droite correspondrait donc, par hypothèse, à une autre structure, actuellement non inventoriée.
Mais avant de passer à cette quatrième droite, voyons maintenant s'il est possible de trouver quelque rapport entre le point de convergence (souterrain) des conduits sud et le point de convergence (céleste). Ce rapport se fait jour, en effet. Et de quelle façon... Les "engendrements géométriques", pour reprendre le mot de Georges Vermard, sont saisissants.
Déterminons, d'abord, le point de rencontre de la ligne horizontale passant par le point de convergence (ci-dessous cerclé en vert) des conduits sud (tracés en rouge) avec la ligne verticale à l'aplomb du point de convergence (également cerclé en vert) des conduits nord (tracés en bleu). A partir de ce point, on peut tracer une droite, de même inclinaison que la pente de la Pyramide (51°51', ici en valeur approchée) possédant plusieurs propriétés.
Tout d'abord, elle intersecte la ligne du conduit-Reine avec un angle de 45°.

On trace ensuite une ligne symétrique à la précédente, toujours, donc, de même inclinaison que l'apothème de la Pyramide. La portion rectiligne du Puits semble se trouver encore directement "concernée" (partie indiquée par une flèche).

Prolongeons maintenant la ligne nord de ce triangle, figurant une sorte de "pyramide bis", jusqu'au niveau du sommet de la Pyramide elle-même, et traçons encore une fois sa droite symétrique, côté sud : le sommet de cette "pyramide bis" est à l'aplomb de l'entrée, tandis que sa ligne d'apothème sud intersecte la ligne du conduit-Roi sud sur l'axe, au niveau de la voûte-Reine :
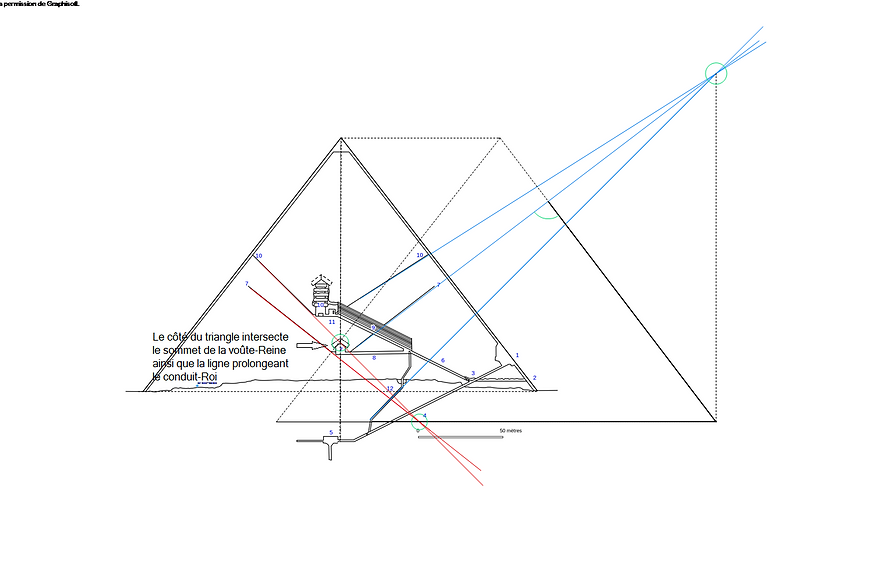

Ce ne sont encore là que les prémices d'un ensemble de concordances et de propriétés inhérentes à la position des deux points de convergence et à leur relation...
Ci-dessous, nous voyons qu'il est possible de joindre le milieu de la base de la "pyramide bis" et le sommet de la voûte-Reine, par une ligne (en vert) parallèle au Couloir ascendant et à la Grande Galerie :

Passons maintenant à notre "Quatrième droite".
Elle n'est pas matérialisée, comme les trois autres, par une structure connue (conduits et Puits). Il ne serait guère étonnant qu'il n'y ait tout simplement pas de telle structure. Le conduit-Reine est de même longueur que le conduit-Roi, mais il "apparaît", d'une certaine façon, plus court que son vis-à-vis supérieur, étant "arrêté" avant la paroi. La portion rectiligne du Puits est, quant à elle, véritablement et nettement plus courte que les conduits. On peut songer à une certaine logique selon laquelle les structures supportées respectivement (et de haut en bas, successivement) par ces quatre droites, seraient de plus en plus réduites, jusqu'à finalement disparaître dans le cas de la quatrième, qui ne supporterait rien.
Symboliquement, la cohérence de cet "enchaînement" serait en rapport avec le caractère "occulte" de la Quatrième chambre : les trois droites supérieures supportent des conduits ou un "puits" menant à (ou dirigé vers) des chambres connues et accessibles, mais il n'y aurait pas de canal ou de couloir, pas de structure concrète sur la quatrième droite, menant à (ou indiquant) une chambre plus secrète.
Quoi qu'il en soit, comment tracer cette droite, à partir du Point Focal Céleste, d'une façon qui ne procède pas d'un choix arbitraire ? Elle partira, comme les trois autres, du Point Focal Céleste ; ce point est acquis. Quelle sera donc son inclinaison ? Essayons, encore une fois, l'angle de la Pyramide elle-même... Deux points d'intersection significatifs se font jour, si nous donnons à cette droite une inclinaison de 51°50 (en valeur suffisamment approchée) :
1) avec le haut de l'entrée (par où passe également, nous l'avons vu, l'axe de la "Pyramide bis" qui se confond avec le côté vertical sud d'un Rectangle d'or) ; ce point se trouve au niveau du sommet de la voûte-Reine,
2) avec le carrefour Couloir ascendant/Descenderie.

Il ne nous reste plus qu'à prolonger cette droite, en bonne logique, jusqu'à la ligne axiale de la Pyramide, et à postuler que ce point correspond à la localisation d'une chambre profondément enfouie dans les entrailles de Gizeh...
Nous aurions ainsi quatre chambres superposées : deux dans la maçonnerie, deux souterraines ; deux axiales, deux décalées par rapport à l'axe.
J'ai donné, il y a deux ans à peu près, dans Nexus, d'autres éléments qui corroborent - ou qui du moins ne contredisent pas - cette hypothèse.
Mes dernières réflexions, toutefois, m'ont conduit à concevoir une autre possibilité. Elle n'est pas éloignée de la précédente ; la Quatrième chambre se trouverait, alors, un peu plus haut.
Sa position (ci-dessous, cerclée en pointillés marrons) serait alors fonction d'une sixième droite issue du Point Focal Céleste, dont l'inclinaison serait celle du Triangle d'or : 72°. A partir du point où cette sixième droite touche la ligne de sol, une ligne parallèle au Couloir descendant rejoindrait la circonférence du cercle vert (dont le centre est donné, rappelons-le, par le Point de convergence souterrain) là où il intersecte la base du triangle rouge. Ce triangle, on le voit, est intérieur au grande cercle rouge dont le rayon = la hauteur de la Pyramide. Le sommet de la chambre pourrait alors se trouver au point où le cercle vert intersecte le carré tracé à partir du Rectangle d'or.

Il n'est pas exclu, dans cette hypothèse, que la chambre, de dimension sensiblement égale à la Chambre haute ("du Roi"), "plafonds" compris, englobe la position précédemment définie. C'est que nous voyons sur cette dernière figure, où se trouve également représentée la position d'un couloir d'accès selon une septième droite dont l'inclinaison serait celle des grands côtés du triangle Dy.
